ML_002：Google Machine Learning 在线速成课程学习笔记之二

在线课程地址：https://developers.google.com/machine-learning

3. 深入了解机器学习

下图是蝉每分钟的鸣叫声和温度方面的数据关系：

毫无疑问，这是一个线性关系：

如何确定模型的优劣？

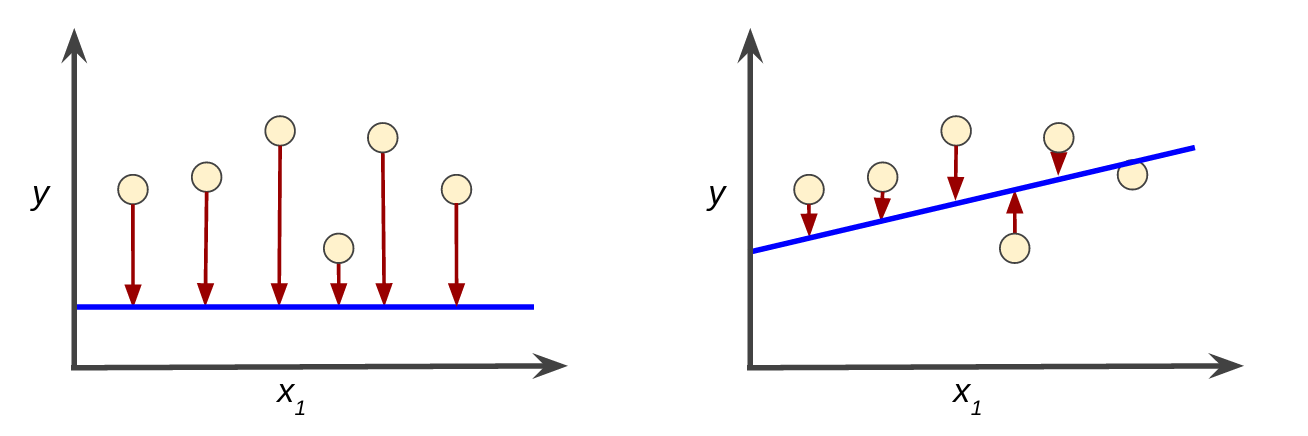
简单来说，训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值。在监督式学习中，机器学习算法通过以下方式构建模型：检查多个样本并尝试找出可最大限度地减少损失的模型；这一过程称为经验风险最小化。

均方误差 (MSE) 指的是每个样本的平均平方损失。

要计算 MSE，请求出各个样本的所有平方损失之和，然后除以样本数量。

虽然 MSE 常用于机器学习，但它既不是唯一实用的损失函数，也不是适用于所有情形的最佳损失函数。

3.1 降低损失：迭代方法

为了训练模型，我们需要一种可降低模型损失的好方法。迭代方法是一种广泛用于降低损失的方法，而且使用起来简单有效。

迭代策略在机器学习中的应用非常普遍，这主要是因为它们可以很好地扩展到大型数据集。
“模型”部分将一个或多个特征作为输入，然后返回一个预测值作为输出。
应该设置哪些初始值？对于线性回归问题，事实证明初始值并不重要，可以随机选择值。

最后，我们来看图的“计算参数更新”部分。机器学习系统就是在此部分检查损失函数的值，并生成新的特征权重值。现在，假设这个神秘的绿色框会产生新值，然后机器学习系统将根据所有标签重新评估所有特征，为损失函数生成一个新值，而该值又产生新的参数值。这种学习过程会持续迭代，直到该算法发现损失可能最低的模型参数。通常，您可以不断迭代，直到总体损失不再变化或至少变化极其缓慢为止。这时候，我们可以说该模型已收敛。

假设我们有时间和计算资源来计算权重的所有可能值的损失。对于我们一直在研究的回归问题，所产生的损失与权重的图形始终是凸形。换言之，图形始终是碗状图，如下所示：

凸形问题只有一个最低点；即只存在一个斜率正好为 0 的位置。这个最小值就是损失函数收敛之处。

3.2 梯度下降法

通过计算整个数据集中  每个可能值的损失函数来找到收敛点这种方法效率太低。我们来研究一种更好的机制，这种机制在机器学习领域非常热门，称为梯度下降法。

请注意，梯度是一个矢量，因此具有以下两个特征：方向和大小。

梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步，以便尽快降低损失。

3.3 降低损失：学习速率

梯度下降法算法用梯度乘以一个称为学习速率（有时也称为步长）的标量，以确定下一个点的位置。

超参数是编程人员在机器学习算法中用于调整的旋钮。大多数机器学习编程人员会花费相当多的时间来调整学习速率。如果您选择的学习速率过小，就会花费太长的学习时间：

如何确定“金发姑娘”学习速率呢？

在实践中，成功的模型训练并不意味着要找到“完美”（或接近完美）的学习速率。我们的目标是找到一个足够高的学习速率，该速率要能够使梯度下降过程高效收敛，但又不会高到使该过程永远无法收敛。

3.4 降低损失：随机梯度下降法

在梯度下降法中，批量指的是用于在单次迭代中计算梯度的样本总数。到目前为止，我们一直假定批量是指整个数据集。就 Google 的规模而言，数据集通常包含数十亿甚至数千亿个样本。此外，Google 数据集通常包含海量特征。因此，一个批量可能相当巨大。如果是超大批量，则单次迭代就可能要花费很长时间进行计算。

包含随机抽样样本的大型数据集可能包含冗余数据。实际上，批量大小越大，出现冗余的可能性就越高。一些冗余可能有助于消除杂乱的梯度，但超大批量所具备的预测价值往往并不比大型批量高。

如果我们可以通过更少的计算量得出正确的平均梯度，会怎么样？通过从我们的数据集中随机选择样本，我们可以通过小得多的数据集估算（尽管过程非常杂乱）出较大的平均值。 随机梯度下降法 (SGD) 将这种想法运用到极致，它每次迭代只使用一个样本（批量大小为 1）。如果进行足够的迭代，SGD 也可以发挥作用，但过程会非常杂乱。“随机”这一术语表示构成各个批量的一个样本都是随机选择的。

每次只随机选出一个样本来计算梯度？只要迭代次数够多，也可以快速收敛。

小批量随机梯度下降法（小批量 SGD）是介于全批量迭代与 SGD 之间的折衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的杂乱样本数量，但仍然比全批量更高效。

为了简化说明，我们只针对单个特征重点介绍了梯度下降法。请放心，梯度下降法也适用于包含多个特征的特征集。